Linear Mixed Effects Model: A Comprehensive Guide

Introduction to Linear Mixed Effects Models (LMM)

Linear Mixed Effects Models (LMM) have become indispensable tools in data analysis, particularly when dealing with complex, hierarchical, or repeated measures data. These models extend traditional linear models by incorporating both fixed and random effects, allowing for greater flexibility and accuracy when analyzing data with grouped structures. LMMs are commonly used in fields such as biostatistics, ecology, psychology, and social sciences.

In this comprehensive guide, we will explore the fundamentals of LMM, the advantages of using them, practical examples of implementation in OriginPro, and key insights into interpreting the results.

Linear Mixed Effects Model (LMM) in OriginPro

Download the LMM App for OriginPro

Enhance your statistical analysis in OriginPro with the free Linear Mixed Effects Model (LMM) App. Download it directly from the Origin Lab website: 👉 Download LMM App for OriginPro

Understanding the Components of LMM

Fixed Effects

Fixed effects represent consistent and predictable influences on the dependent variable. These effects are assumed to be constant across all observations. For example, in a plant growth study, fertilizer type may be treated as a fixed effect because its influence on growth is consistent across all plots.

Random Effects

Random effects account for variability across groups or subjects that are not explicitly modeled. These effects introduce random variations that help explain differences in observations due to unmeasured factors. In the plant growth example, differences in growth between individual plots can be modeled as random effects.

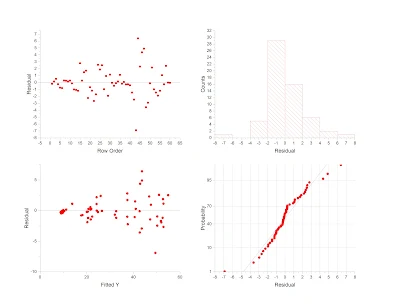
Residuals

Residuals are the unexplained differences between the observed and predicted values. In LMM, residuals capture the random noise that remains after accounting for both fixed and random effects.

Intercept

The intercept in an LMM represents the expected value of the response variable when all predictors are set to zero. It serves as a baseline for interpreting other model coefficients.

Why Choose Linear Mixed Effects Models?

Addressing Non-Independence in Data

LMMs are particularly useful when observations are not independent, a common scenario in repeated measures or nested designs. For instance:

• In clinical trials, patient measurements taken over time are likely correlated.
• In ecological studies, measurements taken from the same plot or location introduce dependencies.
• In educational research, student test scores are often nested within classrooms or schools.

Advantages of LMM

• Flexibility: LMMs can handle unbalanced datasets with missing values more effectively than traditional linear models.
• Hierarchical Data: LMMs naturally model data with nested or hierarchical structures.
• Reduced Risk of Type I Error: By incorporating random effects, LMMs reduce the likelihood of falsely detecting significant effects.
• Improved Model Fit: LMMs account for both within-group and between-group variability, leading to more accurate predictions.

Fitting a Linear Mixed Effects Model in OriginPro

Interpreting the Output

Applications of LMM in Biostatistics

Ecological Research

Ecologists frequently use LMM to analyze plant or animal growth across different environmental conditions. LMM accounts for plot-level variability, ensuring that results reflect genuine treatment effects rather than site-specific differences.

Clinical Trials

LMMs are vital for analyzing patient data collected over multiple visits. Random effects capture individual patient variability, improving the accuracy of treatment effect estimates.

Education and Social Sciences

LMMs help analyze student performance data collected from different schools or classrooms. By modeling school-level random effects, LMMs account for differences in educational environments.

Common Challenges and Solutions

Overfitting

Overfitting occurs when the model captures noise rather than true effects. To mitigate this, limit the number of random effects or use cross-validation.

Interpretation Difficulties

LMM output can be complex, especially for non-statisticians. Focus on effect sizes, confidence intervals, and visualizations to convey results more effectively.

Computational Complexity

Fitting LMMs to large datasets can be computationally intensive. Use parallel processing or reduce the dataset size by aggregating data at higher levels.

Conclusion

Linear Mixed Effects Models offer a robust framework for analyzing data with complex structures. By incorporating both fixed and random effects, LMMs provide deeper insights into data variability and ensure more accurate statistical inferences. Researchers across fields such as biostatistics, ecology, and education rely on LMMs to address challenges in hierarchical and repeated measures data.